Physics of Language Models: Understanding hidden reasoning process

Are language models just memorizing, or is there something deeper going on?

You know that feeling when you’re solving a math problem and everything just clicks? You start connecting the dots, working through each step until you land on the answer. Well, my gut says language models might be doing something similar or, in some cases, something way more complex.

We’re used to seeing large language models (LLMs) churn out math solutions or generate code, but what’s really happening behind the scenes? Are these models actually reasoning like we do, or are they simply remixing patterns from their training? And, more intriguingly, when these models make mistakes, what’s going wrong in their "thought process"?

The study plan is to dig deep into these questions using controlled experiments. Here’s what we will uncover:

1. Do language models truly develop reasoning skills or is it all memorization?
2. What does the model’s internal reasoning process look like, and how is it different from human reasoning?
3. Can models trained on specific datasets like GSM8K generalize their skills to harder, unseen problems?
4. What causes models to make mistakes during reasoning?
5. Does the depth of the model (number of layers) matter more than its width (neurons per layer) in order to solve complex reasoning problems?

This research takes a principled approach to understanding the model's internal processes. The team designed synthetic math datasets and probing techniques (we'll get into that later) to see how well models tackle reasoning tasks. And here’s what they found:

Result 1: These models can solve out-of-distribution problems, including those requiring longer reasoning chains than seen in training.

Result 2: The models don’t just solve problems; they’re efficient about it, often generating the shortest possible solutions, skipping unnecessary steps that is very much the opposite of memorization.

Discovering the Model’s “Mental Process”:

What’s fascinating is how the models seem to have their own internal mental process. It’s like watching someone figure something out: there are moments of reasoning that feel eerily human, and then there are completely unexpected behaviors that might hint at something deeper, possibly the early sparks of AGI.

The most significant finding lies in uncovering the model's internal "mental process", which mirrors human reasoning but also introduces new, unexpected skills:

1. Preprocessing: Before starting to generate any solution, models internally preprocess all necessary parameters like humans. Picture how you might jot down numbers or formulas on a scrap of paper before diving into a math problem. These models do the same, but mentally, without explicit instructions.
2. All-Pair Dependency: Here’s where things get wild: models are calculating the relationships between all variables while solving a given problem, even when they don’t need to. This ability to compute relationships between objects "mentally" suggests a level of reasoning skill that exceeds humIn fact, this skill might be one of the first glimpses of AGI, since humans usually only consider what's necessary to reach the goal.
3. Backward Reasoning: Similar to how we work backwards from a goal, models trace the steps needed to reach a solution, reverse-engineering the problem to find the path forward.

Depth vs. Width in Language Models:

One of the biggest revelations from this research is how it challenges the common belief that "bigger is better” when it comes to neural networks. We’ve all heard that more neurons (width) mean better performance, right? Turns out, depth (number of layers) plays a way more crucial role in solving tough problems than just throwing more neurons at each layer.

For example:

• A 16-layer, 576-dim model outperformed a 4-layer, 1920-dim one in more complex reasoning tasks, despite the latter being twice as large. The deeper model’s longer reasoning chain gave it the edge in solving complex, multi-step problems. More layers meant the model could extend its reasoning further, making it better at handling harder tasks. This suggests that the depth of the network allows it to capture hierarchical structures and long-term dependencies, which are critical for reasoning tasks.

Model Width: While width (the number of neurons in each layer) can help with tasks that require more pattern recognition or brute-force computation, it does not contribute as much to the model’s ability to solve complex, multi-step reasoning problems.

Understanding depth vs width a little bit more in detail

In language models, the choice between depth and width significantly influences their effectiveness in handling different types of tasks.

Wide models, with a greater number of neurons per layer, are particularly well-suited for tasks involving pattern recognition. This type of model excels at identifying regularities and associations in data, whether it's recognizing shapes in images or detecting common phrases in text. The increased number of neurons allows the model to capture a diverse array of features from the input data simultaneously, with each neuron acting as a specialized detector for specific patterns. This parallel processing capability enables wide models to efficiently extract and differentiate between complex patterns within a single layer, making them ideal for tasks that require extensive feature extraction, like image classification or keyword spotting in large text corpora.

On the other hand, deep models are more effective for logical and cognitive tasks, which demand a structured, sequential approach to problem-solving. These tasks, such as multi-step arithmetic problems or logical deductions, require the model to maintain context and track dependencies across several layers. The layered architecture of deep models allows each successive layer to refine and build upon the information from the previous one, creating a coherent chain of reasoning that is essential for handling complex relationships and long sequences.

Understanding Probing and Probing techniques

We have read above that in this study, probing techniques were used to understand the inside of the model and its reasoning.

what do you mean by probing? what are the probing techniques used here?

In general, probing refers to techniques used to inspect and analyze the internal workings of something, basically a thorough search process. so here, in the context of language models, probing means the same, we go deep into the model understanding it’s internal states and workings.

How V-Probing Works

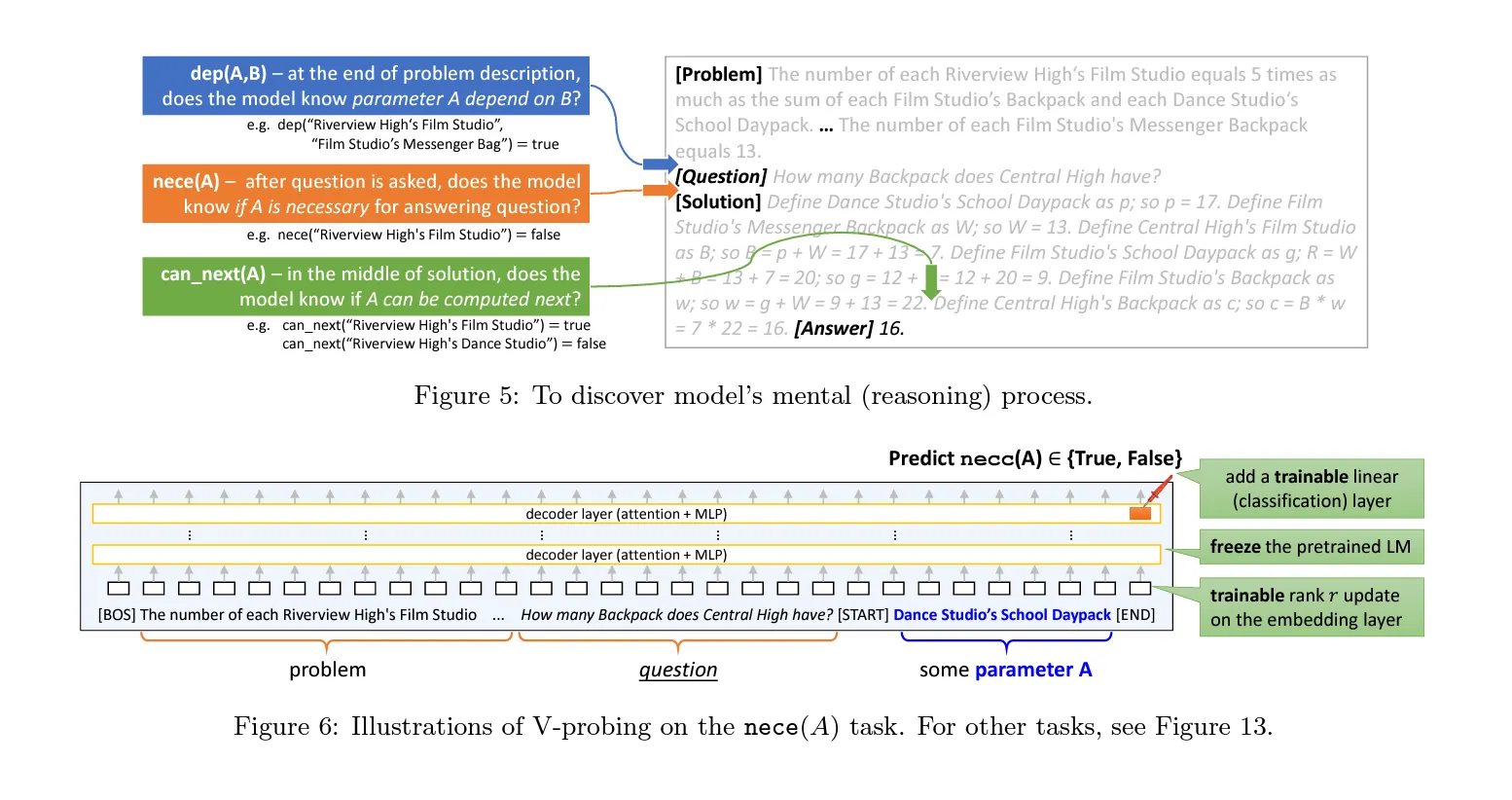
1. Probing Positions: Probing is conducted at various points, depending on the task:
   • For dependency (`dep`) tasks, probing occurs at the end of the problem description to check if the model understands that parameter A depends on B.
   • For necessity (`nece`) tasks, probing happens at the end of the question description to see if the model recognizes that parameter A is necessary.
   • For other tasks, probing is performed at the end of each solution sentence to monitor how the model's internal states evolve throughout the solution process.
2. Standard Linear Probing: Typically, standard linear probing involves freezing a pre-trained model and adding a linear classifier to the hidden states, usually at the last layer. This classifier is then fine-tuned to see if the desired property (like parameter necessity or dependency) is linearly encoded at a specific token position. Used for simpler tasks such as `known(A)` and `value(A)` with lightweight classifiers.
3. V-Probing Enhancements:
   • Handling Conditional Variables: To manage conditional variables like A and A,B, the researchers truncate the math problems to the probing position and append special tokens [START] and [END] around the descriptions of these variables. This setup allows them to probe the model from the [END] token position to check if the desired property is encoded at the last layer.
   • Trainable Rank-8 Update: Unlike standard linear probing, which only adds a linear classifier, V-Probing introduces a small trainable rank-8 linear update on the input embedding layer. This update is fine-tuned alongside the linear classifier to account for the changes in the input structure and to better focus the model on the variables of interest.
4. Freezing and Fine-Tuning: The pre-trained language model's weights are frozen, and only the trainable components (the rank-8 update and the linear classifier) are fine-tuned. This ensures that the probing focuses on extracting information from the existing model representations rather than altering the model’s underlying knowledge.

Come back to this diagram after understanding all the 6 probing parameters to refer back and relate how v-probing is used in this math problem.

Probing Mechanism in the Architecture

To conduct probing, the researchers made specific architectural modifications to the GPT-2 model:

Model used: 12-layer, 12-head, 768-dim GPT2 (a.k.a. GPT2-small)

1. Freezing the Model: The core GPT-2 model's pre-trained weights were frozen.
2. Rotary Positional Embeddings (RoPE): Standard positional embeddings were replaced with RoPE. This modification enabled the model to better capture relative positions and relationships between variables in math problems, crucial for understanding dependencies.
3. Trainable Updates: Rank-8 transformations were added to the input embeddings. (explaining RoPE, rank-8 transformations is out of the scope of this blog, but maybe we can cover in a different blog dedicated to these topics)

How the Model is Being Used in Probing

• Embedding Modification: The modified input embeddings, adjusted using rank-8 transformations, are processed through the frozen GPT-2 model, ensuring that the model’s pre-learned representations are utilized effectively.
• Classification Task: The processed embeddings are fed into lightweight classifiers, which predict properties like parameter necessity and dependencies. This setup ensures focused and efficient probing without altering the model’s fundamental knowledge.

Probing Tasks Explained:

1. Parameter Necessity Probing (`nece(A)`): This probe checks whether the model recognizes that a parameter A is necessary to solve the math problem before it starts generating the solution.
2. Dependency Probing (`dep(A,B)`): The researchers probe the model's internal states to see if it has computed dependencies between parameters before answering. This mimics how humans might mentally organize which variables depend on others when solving problems.
3. Known Value Probing (`known(A)`): This probe checks whether the model knows that a particular parameter A has already been computed.
4. Parameter Value Probing (`value(A)`): During the solution generation process, the model may compute the value of A. This probe tests if the model correctly stores and recalls that value.
5. Next Step Probing (`can_next(A)`): This probe checks whether the model has enough information to compute parameter A in the the next step in the solution, i.e., whether all the prerequisites for calculating A have been met.
6. Necessity of Next Step Probing (`nece_next(A)`): This probe assesses if the model identifies a parameter A as both ready to be computed and necessary for solving the problem.

Explaining the Model’s Mistakes

The researchers analyzed the relationship between the model’s internal states (probed using V-Probing) and the errors in its generated solutions. They focused on two main types of errors:

1. Unnecessary Parameters in Correct Solutions: The model sometimes generates correct answers but includes unnecessary parameters or steps. This typically occurs because the model misjudges the necessity of certain parameters during its "mental planning phase." The researchers found that in out-of-distribution tasks, pre-trained models often predict some parameters as necessary (`nece(A)=true`) even when they aren’t needed. This leads to extra steps in the solution, highlighting that the model’s mistakes stem from incorrect internal predictions rather than random generation errors.
2. Incorrect Answers Due to Wrong Parameter Predictions: When the model produces incorrect answers, the errors often originate from its internal misjudgment about whether a parameter is ready to be computed. Specifically, the model incorrectly predicts `nece_next(A)` or `can_next(A)` as true, indicating that it believes certain steps are appropriate when they are not. These errors occur before the model even begins generating the solution, suggesting that the model’s internal planning, not just the generation process, is flawed. Many of the reasoning mistakes made by the language model are systematic, arising from errors in its internal mental process rather than being random mistakes during the generation phase.

Conclusion

This research offers the first glimpse of AGI-like capabilities, with models demonstrating complex reasoning and mental processes. Despite their limitations, these findings provide hope for even more advanced AI in the future.